『5乗とか絶対にムリです。2乗が限界です。』
という悩みに、答えていきます。
こんにちは、エイタです。
面倒くさがりなので、手放して生きてます。
今回は、「5乗を展開せよのムズい解き方」を手放していきます。
1.(2x-3)の5乗を展開せよ
本日は、この問題を解きます。

5乗(じょう)って何?
5乗は、(かっこ)の中を5回かけるってことです。
今回の問題で言えば、こんな感じ。
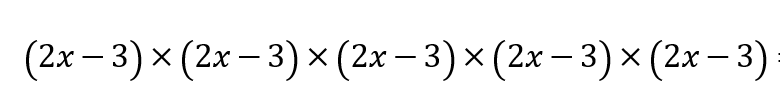
展開(てんかい)って何?
展開とは、「ひとくくりになってるものを、広げること」です。
つまり、(かっこ)の無い状態にしろという意味です。なのでさっきの式を、(かっこ)がなくなるまで計算すれば良いだけです。
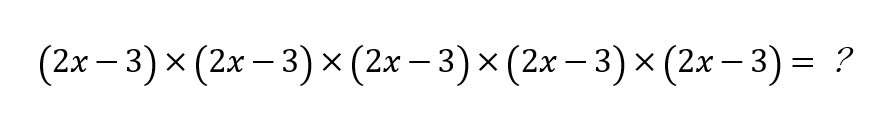
これをゴリゴリ計算していけば、答えがでます。ちなみに答えはコレです。
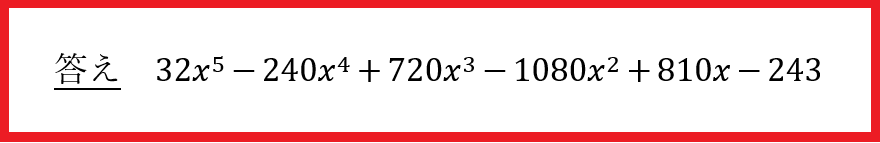
つまり、「5乗を展開しろ」と言われたら、5回かけて、(かっこ)をなくせば良いのです。
言ってることは簡単なので、たぶん理解できたと思います。
ただ、バカ正直に計算すると、めちゃダルいです。(一応、計算式を記事の最後に載せておきます。)そこで今回、裏技チックな方法を紹介します。
5乗だけ?
今回紹介する方法は、5乗はもちろん、2乗や3乗、10乗、「それ以上でも」使えます。
非常にコスパが良いので、ぜひ覚えていってください。
2.「(2x-3)の5乗を展開せよ」の解き方

覚えることは3つ
これを解くにあたって、覚えることは以下の3つです。
1のピラミッド
↓
ピラミッドの数字×〇×□
↓
〇と□のカウントダウン
1つずつ解説しながら、答えまでやっていきましょう。
1のピラミッドとは?

これが「1のピラミッド」です。1を3つ使ってるから、勝手に僕がそう呼んでるだけです。正式名称ではありません。気にしないでください。
で、このピラミッドは成長します。5乗の場合、以下のピラミッドを使います。
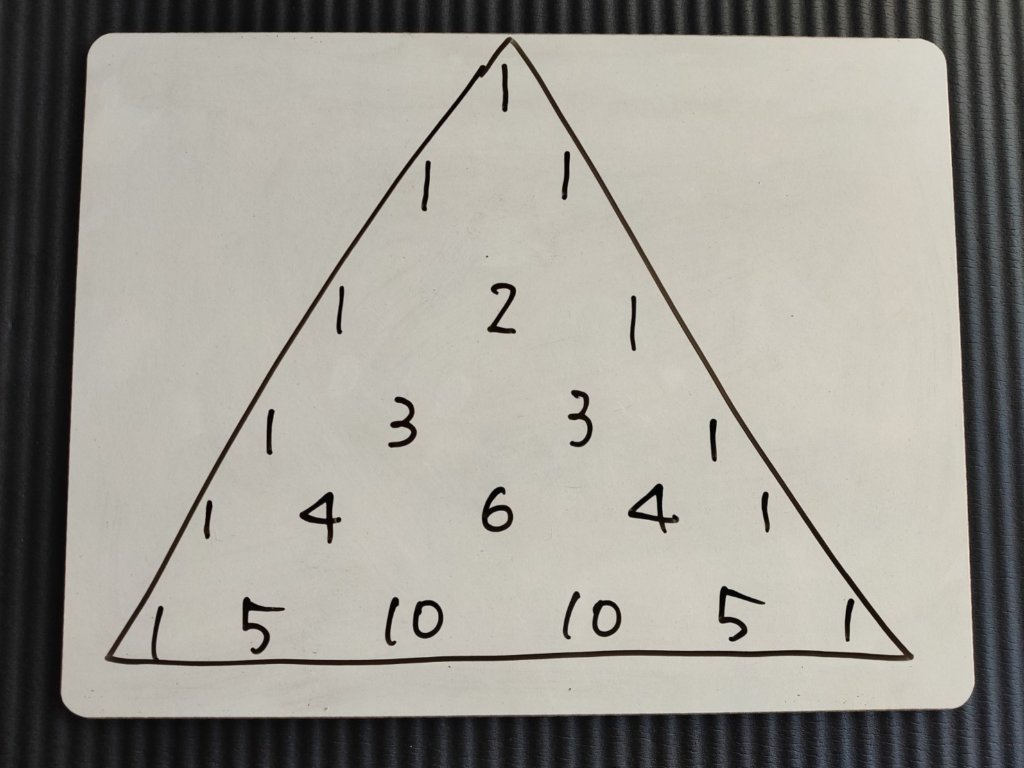
ピラミッドの中の数字ですが、「まさか覚えろと?」いえ、その必要はありません。
最初の「1のピラミッド」さえ書けてれば、あとは簡単です。
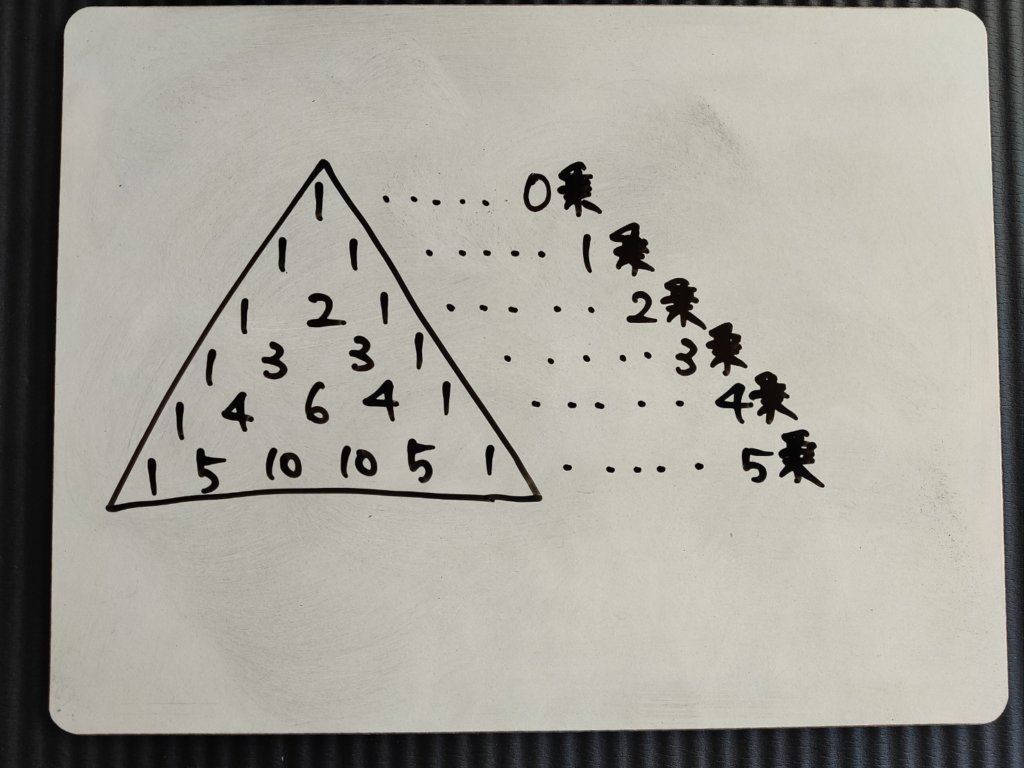
ピラミッドの端っこはずっと1で、中の数字は、上の2つを足すだけです。これなら、いくらでも増殖可能です。
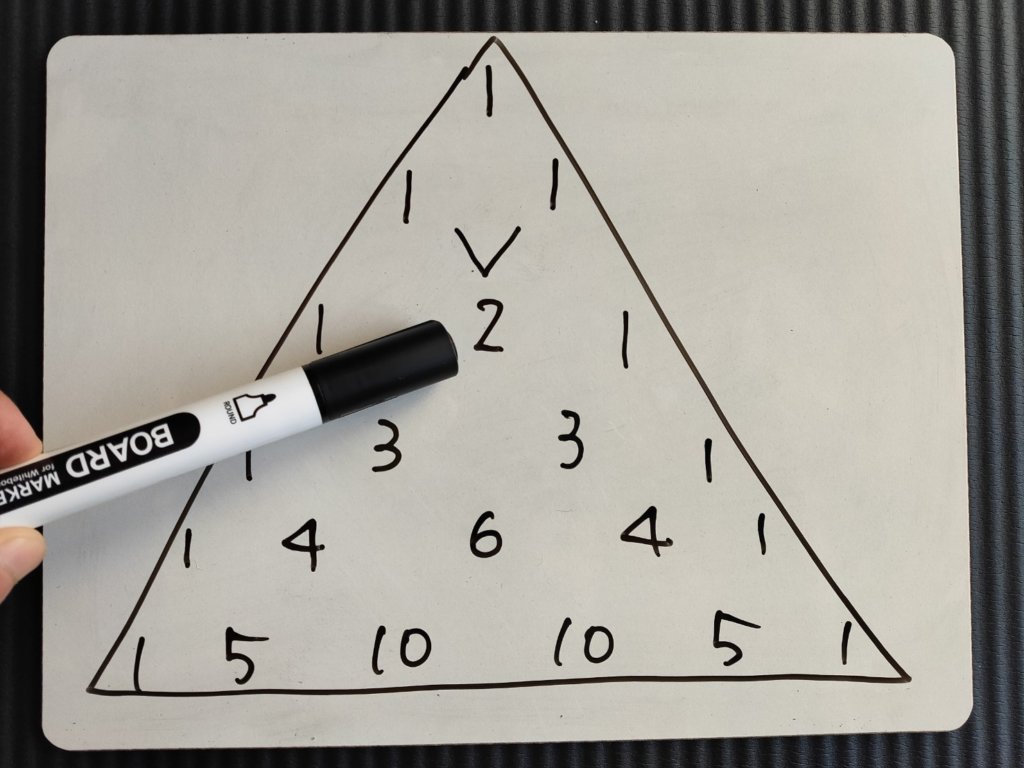
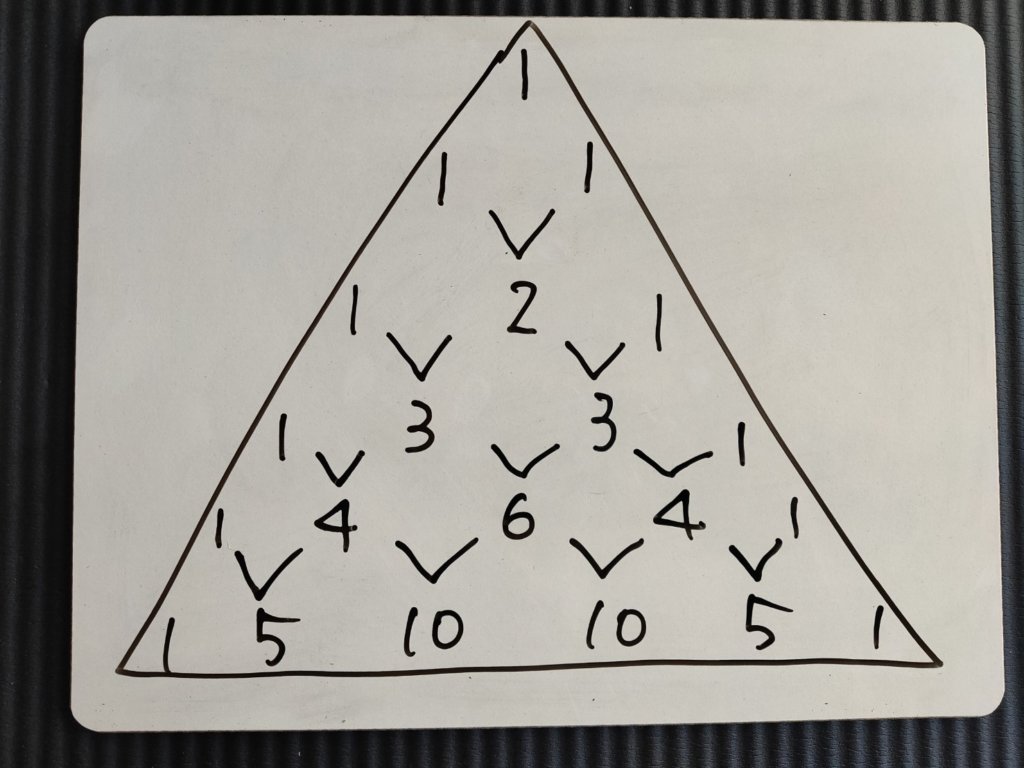
簡単ですよね。
で、今回の問題が5乗なので、ピラミッドの5乗の列を使います。この「1・5・10・10・5・1」を使って式を作っていきます。
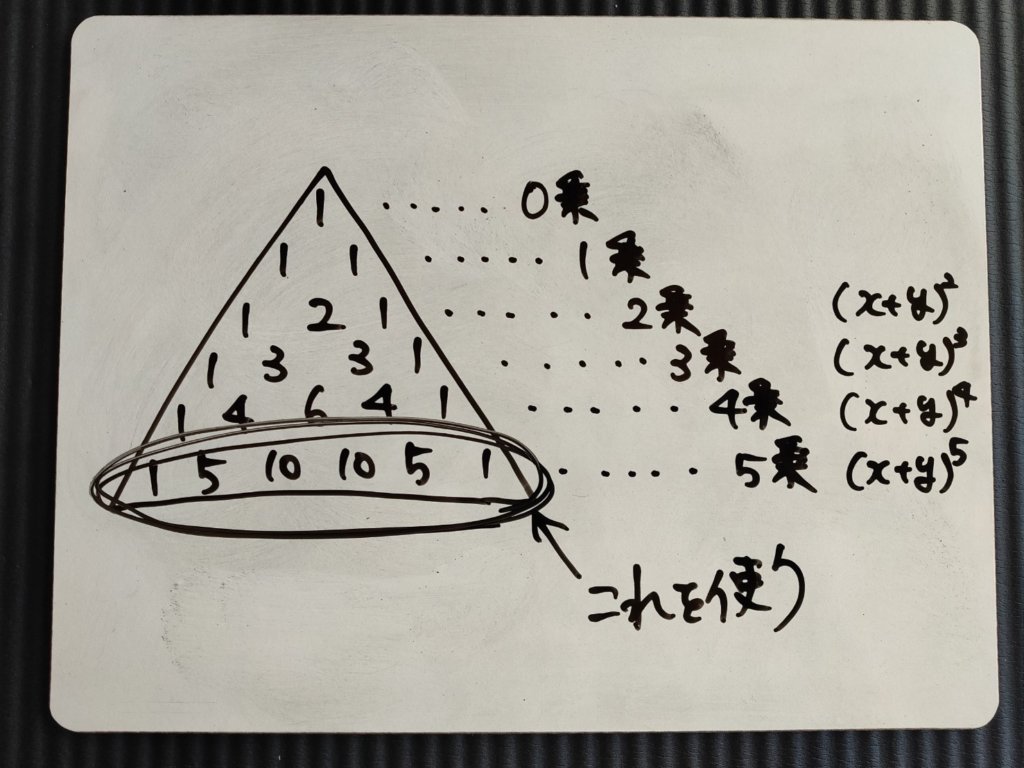
ピラミッドの数字×〇×□とは?
使い方は、こんな感じです。
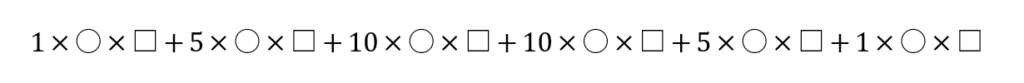
『ピラミッドの数字×〇×□』を「+」で繋げただけです。〇と□は分かりやすいように、僕が勝手に使ってるだけです。やり方が分かって、不要そうでしたら無視してください。
1点注意がありまして、右からでも左からでも良いので、ピラミッドの数字の順番だけは替えないでください。宜しくお願いします。
〇と□のカウントダウンとは?
では次です。
〇に5乗、4乗、3乗…と書いていきます。「5乗を展開せよ」なので、5からスタートです。カウントダウンする感じです。
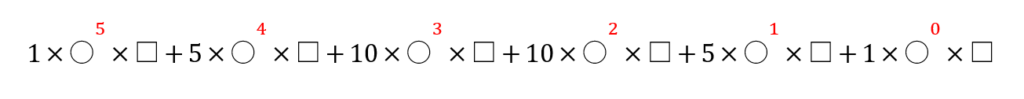
次は□に、0乗、1乗、2乗…と書いていきます。〇と逆カウントしてください。
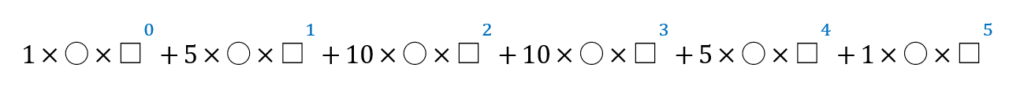
両方合わせるとこんな感じです。
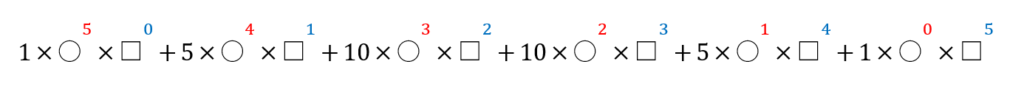
これで式はほぼ完成です。あとは、僕が適当に〇と□と書いてたところに、数字を入れていきます。
もう1度、問題を見てください。
〇は前の部分(2x)、□は後ろの部分(-3)のことです。慣れてきたら、最初から数字を入れてOKです。
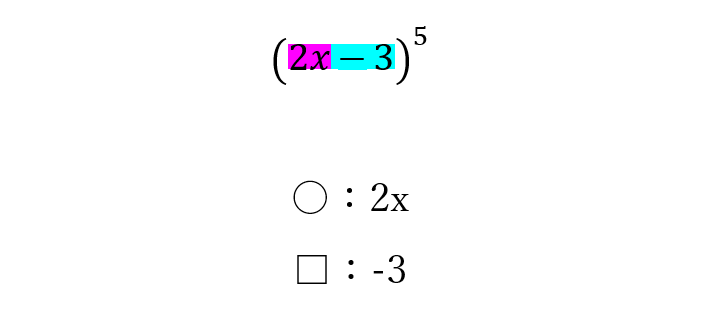
これで式が完成です
完成した式がこちらです。
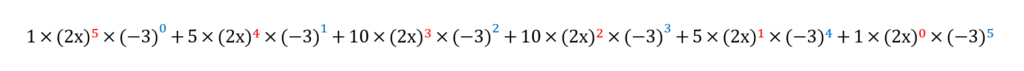
「ウゲっ」となりそうですが、やってみると案外そうでもないです。これが「5乗を展開せよ」の簡単な解き方です。
なお、ピラミッドを伸ばせば、10乗とかでも対応できます。試してみてください。
「あれ?0乗って何になるんだっけ?」と思った方のために、この1文を提供して終わりにします。
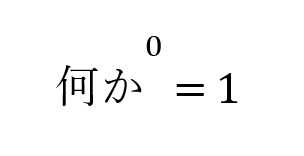
3.余談です(テスト出ません)
パスカルさん

余談ですがさっきのピラミッドは、「パスカルの三角形」という名前がついてます。
そう、パスカルさんが発表したからです。
ちなみにパスカルさんは39歳で亡くなったそうです。早いですよね。
(ウィキペディアによると)17歳の時に、計算機を作るのに没頭し過ぎて、寿命が縮まったらしいです。そんなことあるんですね…。
ゴリゴリ計算してみた
冒頭で言った、「ゴリゴリやれば解ける」を実際にやってみました。

なかなかな量ですよね。ここまで長いと、計算ミスが出やすいので、あまりオススメはしません。
ですが、もしピラミッドを忘れた場合は、ゴリゴリやりましょう。
とはいえ、5乗でこの量ですから、10乗とかの問題が出たら、さすがに心折れそうですが…。
まとめ
・5乗を展開せよは、かっこをなくしての意
・ゴリゴリ計算すれば答えは出る
・でも、ピラミッドを使った方が簡単
今回の問題は、数研の青チャートから引用しました。


コメント